Connaissez-vous le problème mathématique du sofa? C’est la tentative, tout à fait sérieuse, de calculer quelle est la taille idéale et la longueur maximale du sofa que l’on peut déménager dans un corridor — ou un escalier — qui tourne à angle droit.
Comme quoi le problème est aussi difficile à résoudre que certaines des plus grandes énigmes mathématiques, il a été mis de l’avant pour la première fois en 1966 par le mathématicien Leo Moser. Et ce n’est qu’à présent qu’un autre mathématicien vient de proposer ce qui pourrait être la solution définitive.
Quiconque a déménagé alors qu’il devait traverser un corridor ou un escalier étroit n’avait pas besoin de mathématiciens pour lui dire qu’un sofa était un problème en soi à cause de sa forme allongée —et on ne parle même pas de son poids. Mais certains sofas sont moins problématiques que d’autres. Dans ce nouvel article, déposé sur la plateforme de prépublication ArXiv, Jineon Baek de l’Université Yonsei en Corée du Sud, tranche pour la forme « fer à cheval ».
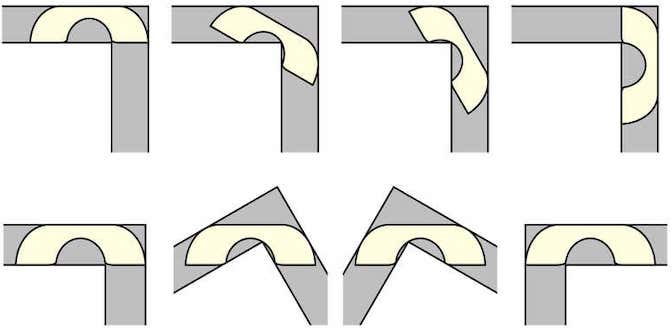
Il s’agit de ce qu’on appelle le sofa de Gerver, du nom de Joseph Gerver, de l’Université Rutgers, au New Jersey, qui avait suggéré que cette forme était celle qui permettait le plus long sofa possible, dans un corridor d’un mètre de large avec un angle droit. Mais il a fallu à Baek plus de 100 pages d’équations et de géométrie pour en faire la démonstration.
« J’ai consacré beaucoup de temps à ça », concède Baek. Qui arrivera peut-être mieux préparé à son prochain déménagement.






